1 Introduction
Information flow describes how data influences other data within a program. Information flow has applications to security, such as information flow control [], and to developer tools, such as program slicing []. Our goal is to build a practical system for analyzing information flow, meaning:
Applicable to common language features: the language being analyzed should support widely used features like pointers and in-place mutation.
Zero configuration to run on existing code: the analyzer must integrate with an existing language and existing unannotated programs. It must not require users to adopt a new language designed for information flow.
No dynamic analysis: to reduce integration challenges and costs, the analyzer must be purely static — no modifications to runtimes or binaries are needed.
Modular over dependencies: programs may not have source available for dependencies. The analyzer must have reasonable precision without whole-program analysis.
As a case study on the challenges imposed by these requirements, consider analyzing the information that flows to the return value in this C++ function:
Here, a key flow is that v2 is influenced by v: (1) push_back mutates v2 with *x as input, and (2) x points to data within v. But how could an analyzer statically deduce these facts? For C++, the answer is by looking at function implementations. The implementation of push_back mutates v2, and the implementation of begin returns a pointer to data in v.
However, analyzing such implementations violates our fourth requirement, since these functions may only have their type signature available. In C++, given only a function's type signature, not much can be inferred about its behavior, since the type system does not contain information relevant to pointer analysis.
Our key insight is that ownership types can be leveraged to modularly analyze pointers and mutation using only a function's type signature. Ownership has emerged from several intersecting lines of research on linear logic [], class-based alias management [], and region-based memory management []. The fundamental law of ownership is that data cannot be simultaneously aliased and mutated. Ownership-based type systems enforce this law by tracking which entities own which data, allowing ownership to be transferred between entities, and flagging ownership violations like mutating immutably-borrowed data.
Today, the most popular ownership-based language is Rust. Consider the information flows in this Rust implementation of copy_to:
Focus on the two methods push and iter. For a Vec<i32>, these methods have the following type signatures:
To determine that push mutates v2, we leverage mutability modifiers. All references in Rust are either immutable (i.e. the type is &T) or mutable (the type is &mut T). Therefore iter does not mutate v because it takes &self as input (excepting interior mutability, discussed in Section 4.3), while push may mutate v2 because it takes &mut self as input.
To determine that x points to v, we leverage lifetimes. All references in Rust are annotated with a lifetime, either explicitly (such as 'a) or implicitly. Shared lifetimes indicate aliasing: because &self in iter has lifetime 'a, and because the returned Iter structure shares that lifetime, then we can determine that Iter may contain pointers to self.
Inspired by this insight, we built Flowistry, a system for analyzing information flow in the safe subset of Rust programs. Flowistry satisfies our four design criteria: (1) Rust supports pointers and mutation, (2) Flowistry does not require any change to the Rust language or to Rust programs, (3) Flowistry is a purely static analysis, and (4) Flowistry uses ownership types to analyze function calls without needing their definition. This paper presents a theoretical and empirical investigation into Flowistry in five parts:
We provide a precise description of how Flowistry computes information flow by embedding its definition within Oxide [], a formal model of Rust (Section 2).
We prove the soundness of our information flow analysis as a form of noninterference (Section 3).
We describe the implementation of Flowistry that bridges the theory of Oxide to the practicalities of Rust (Section 4).
We evaluate the precision of the modular analysis on a dataset of large Rust codebases, finding that modular flows are identical to whole-program flows in 94% of cases, and are on average 7% larger in the remaining cases (Section 5).
We demonstrate the utility of Flowistry by using it to prototype a program slicer and an IFC checker (Section 6).
We conclude by presenting related work (Section 7) and discussing future directions for Flowistry (Section 8). Due to space constraints, we omit many formal details, all auxiliary lemmas, and all proofs. The interested reader can find them in the appendix. Flowistry and our applications of it are publicly available, open-source, MIT-licensed projects at https://github.com/willcrichton/flowistry.
2 Analysis
Inspired by the dependency calculus of , our analysis represents information flow as a set of dependencies for each variable in a given function. The analysis is flow-sensitive, computing a different dependency set at each program location, and field-sensitive, distinguishing between dependencies for fields of a data structure.
While the analysis is implemented in and for Rust, our goal here is to provide a description of it that is both concise (for clarity of communication) and precise (for amenability to proof). We therefore base our description on Oxide [], a formal model of Rust. At a high level, Oxide provides three ingredients:
A syntax of Rust-like programs with expressions and types .
A type-checker, expressed with the judgment using the contexts for types and lifetimes, for type variables, and for global functions.
An interpreter, expressed by a small-step operational semantics with the judgment using for a runtime stack.
We extend this model by assuming that each expression in a program is automatically labeled with a unique location . Then for a given expression , our analysis computes the set of dependencies . Because expressions have effects on persistent memory, we further compute a dependency context from memory locations to dependencies . The computation of information flow is intertwined with type-checking, represented as a modified type-checking judgment (additions highlighted in red):
This judgment is read as, "with type contexts and dependency context , at location has type and dependencies , producing a new dependency context ."
Oxide is a large language — describing every feature, judgment, and inference rule would exceed our space constraints. Instead, in this section we focus on a few key rules that demonstrate the novel aspects of our system. We first lay the foundations for dealing with variables and mutation (Section 2.1), and then describe how we modularly analyze references (Section 2.2) and function calls (Section 2.3). The remaining rules can be found in the appendix.
2.1 Variables and Mutation
The core of Oxide is an imperative calculus with constants and variables. The abstract syntax for these features is below:
Constants are Oxide's atomic values and also the base-case for information flow. A constant's dependency is simply itself, expressed through the T-u32 rule:
T-u32 | |
Variables and mutation are introduced through let-bindings and assignment expressions, respectively. For example, this (location-annotated) program mutates a field of a tuple:
Here, is a variable and is a place, or a description of a specific region in memory. For information flow, the key idea is that let-bindings introduce a set of places into , and then assignment expressions change a place's dependencies within . In the above example, after binding , then is:
After checking "", then is added to and , but not . This is because the values of and have changed, but the value of has not. Formally, the let-binding rule is:
T-let | |
Again, this rule (and many others) contain aspects of Oxide that are not essential for understanding information flow such as the subtyping judgment or the metafunction . For brevity we will not cover these aspects here, and instead refer the interested reader to . We have deemphasized (in grey) the judgments which are not important to understanding our information flow additions.
The key concept is the formula . This introduces two shorthands: first, means "a place with root variable in a context ", used to decompose a place. In T-let, the update to happens for all places with a root variable . Second, means "set to in ". So this rule specifies that when checking , all places within are initialized to the dependencies of .
Next, the assignment expression rule is defined as updating all the conflicts of a place :
T-assign | |
If you conceptualize a type as a tree and a path as a node in that tree, then a node's conflicts are its ancestors and descendants (but not siblings). Semantically, conflicts are the set of places whose value change if a given place is mutated. Recall from the previous example that conflicts with and , but not . Formally, we say two places are disjoint () or conflict () when:
Then to update a place's conflicts in , we define the metafunction to add to all conflicting places . (Note that this rule is actually defined over place expressions , which are explained in the next subsection.)
Finally, the rule for reading places is simply to look up the place's dependencies in :
T-move | |
2.2 References
Beyond concrete places in memory, Oxide also contains references that point to places. As in Rust, these references have both a lifetime (called a "provenance") and a mutability qualifier (called an "ownership qualifier"). Their syntax is:
Provenances are created via a expression, and references are created via a borrow expression that has an initial concrete provenance (abstract provenances are just used for types of function parameters). References are used in conjunction with place expressions that are places whose paths contain dereferences. For example, this program creates, reborrows, and mutates a reference:
Consider the information flow induced by . We need to compute all places that could point-to, in this case , so can be added to the conflicts of . Essentially, we must perform a pointer analysis [].
The key idea is that Oxide already does a pointer analysis! Performing one is an essential task in ensuring ownership-safety. All we have to do is extract the relevant information with Oxide's existing judgments. This is represented by the information flow extension to the reference-mutation rule:
T-assignderef | |
Here, the important concept is Oxide's ownership safety judgment: , read as "in the contexts and , can be used -ly and points to a loan in ." A loan is a place expression with an ownership-qualifier. In Oxide, this judgment is used to ensure that a place is used safely at a given level of mutability. For instance, in the example at the top of this column, if was replaced with , then this would violate ownership-safety because is already borrowed by and .
In the example as written, the ownership-safety judgment for would compute the loan set:
Note that is in the loan set of . That suggests the loan set can be used as a pointer analysis. The complete details of computing the loan set can be found in , but the summary for this example is:
Checking the borrow expression "" gets the loan set for , which is just , and so sets .
Checking the assignment "" requires that is a subtype of , which requires that "outlives" , denoted .
The constraint adds to , so .
Checking "" gets the loan set for , which is:
That is, the loans for are looked up in (to get ), and then the additional projection is added on-top of each loan (to get ).
Then because .
Finally, the loan set for is:
Applying this concept to the T-assignderef rule, we compute information flow for reference-mutation as: when mutating with loans , add to all the conflicts for every loan .
2.3 Function Calls
Finally, we examine how to modularly compute information flow through function calls, starting with syntax:
Oxide functions are parameterized by frame variables (for closures), abstract provenances (for provenance polymorphism), and type variables (for type polymorphism). Unlike Oxide, we restrict to functions with one argument for simplicity in the formalism. Calling a function requires an argument and any type-level parameters and .
The key question is: without inspecting its definition, what is the most precise assumption we can make about a function's information flow while still being sound? By "precise" we mean "if the analysis says there is a flow, then the flow actually exists", and by "sound" we mean "if a flow actually exists, then the analysis says that flow exists." For example consider this program:
First, what can mutate? Any data behind a shared reference is immutable, so only could possibly be mutated, not . More generally, the argument's transitive mutable references must be assumed to be mutated.
Second, what are the inputs to the mutation of ? This could theoretically be any possible value in the input, so both and . More generally, every transitively readable place from the argument must be assumed to be to be an input to the mutation. So in this example, a modular analysis of the information flow from calling would add to but not .
To formalize these concepts, we first need to describe the transitive references of a place. The metafunction computes a place expression for every reference accessible from . If then this just includes unique references, otherwise it includes unique and shared ones.
Here, means "a loan at can be used as a loan at ", defined as and otherwise. Then can be defined as the set of concrete places accessible from those transitive references:
Finally, the function application rule can be revised to include information flow as follows:
T-app | |
The collective dependencies of the input are collected into , and then every unique reference is updated with . Additionally, the function's return value is assumed to be influenced by any input, and so has dependencies .
Note that this rule does not depend on the body of the function , only its type signature in . This is the key to the modular approximation. Additionally, it means that this analysis can trivially handle higher-order functions. If were a parameter to the function being analyzed, then no control-flow analysis is needed to guess its definition.
3 Soundness
To characterize the correctness of our analysis, we seek to prove its soundness: if a true information flow exists in a program, then the analysis computes that flow. The standard soundness theorem for information flow systems is noninterference []. At a high level, noninterference states that for a given program and its dependencies, and for any two execution contexts, if the dependencies are equal between contexts, then the program will execute with the same observable behavior in both cases. For our analysis, we focus just on values produced by the program, instead of other behaviors like termination or timing.
To formally define noninterference within Oxide, we first need to explore Oxide's operational semantics. Oxide programs are executed in the context of a stack of frames that map variables to values:
For example, in the empty stack , the expression "" would first add to the stack. Then executing would update . More generally, we use the shorthand to mean ``reduce to a concrete location , then look up the value of in .''
The key ingredient for noninterference is the equivalence of dependencies between stacks. That is, for two stacks and and a set of dependencies in a context , we say those stacks are the same up to if all with are the same between stacks. Formally, the dependencies of and equivalence of heaps are defined as:
Then we define noninterference as follows:
Let such that:
For , let such that:
Then:
This theorem states that given a well-typed expression and corresponding stacks , then its output should be equal if the expression's dependencies are initially equal. Moreover, for any place expression , if its dependencies in the output context are initially equal then the stack value will be the same after execution.
Note that the context is required to be empty because an expression can only evaluate if it does not contain abstract type or provenance variables. The judgment means "the stack is well-typed under and ". That is, for all places in , then and has type .
The proof of Theorem 1, found in the appendix, guarantees that we can soundly compute information flow for Oxide programs.
4 Implementation
Our formal model provides a sound theoretical basis for analyzing information flow in Oxide. However, Rust is a more complex language than Oxide, and the Rust compiler uses many intermediate representations beyond its surface syntax. Therefore in this section, we describe the key details of how our system, Flowistry, bridges theory to practice. Specifically:
Rust computes lifetime-related information on a control-flow graph (CFG) program representation, not the high-level AST. So we translate our analysis to work for CFGs (Section 4.1).
Rust does not compute the loan set for lifetimes directly like in Oxide. So we must reconstruct the loan sets given the information exported by Rust (Section 4.2).
Rust contains escape hatches for ownership-unsafe code that cannot be analyzed using our analysis. So we describe the situations in which our analysis is unsound for Rust programs (Section 4.3).
4.1 Analyzing Control-Flow Graphs
Example of how Flowistry computes information flow. On the left is a Rust function get_count that finds a value in a hash map for a given key, and inserts 0 if none exists. On the right get_count is lowered into Rust's MIR control-flow graph, annotated with information flow. Each rectangle is a basic block, named at the top. Arrows indicate control flow (panics omitted).
Beside each instruction is the result of the information flow analysis, which maps place expressions to locations in the CFG (akin to in Section 2). For example, the insert function call adds dependencies to *h because it is assumed to be mutated, since it is a mutable reference. Additionally, the switch instructions and _4 variable are added as dependencies to h because the call to insert is control-dependent on the switch.
The Rust compiler lowers programs into a "mid-level representation", or MIR, that represents programs as a control-flow graph. Essentially, expressions are flattened into sequences of instructions (basic blocks) which terminate in instructions that can jump to other blocks, like a branch or function call. Figure 1 shows an example CFG and its information flow.
To implement the modular information flow analysis for MIR, we reused standard static analysis techniques for CFGs, i.e., a flow-sensitive, forward dataflow analysis pass where:
At each instruction, we maintain a mapping from place expressions to a set of locations in the CFG on which the place is dependent, comparable to in Section 2.
A transfer function updates for each instruction, e.g. follows the same rules as in T-assignderef by adding the dependencies of to all conflicts of aliases of .
The input to a basic block is the join of each of the output for each incoming edge, i.e. . The join operation is key-wise set union, or more precisely:
We iterate this analysis to a fixpoint, which we are guaranteed to reach because forms a join-semilattice.
To handle indirect information flows via control flow, such as the dependence of h on contains_key in Figure 1, we compute the control-dependence between instructions. We define control-dependence following : an instruction is control-dependent on if there exists a directed path from to such that any in is post-dominated by , and is not post-dominated by . An instruction is post-dominated by if is on every path from to a return node. We compute control-dependencies by generating the post-dominator tree and frontier of the CFG using the algorithms of and , respectively.
Besides a return, the only other control-flow path out of a function in Rust is a panic. For example, each function call in Figure 1 actually has an implicit edge to a panic node (not depicted). Unlike exceptions in other languages, panics are designed to indicate unrecoverable failure. Therefore we exclude panics from our control-dependence analysis.
4.2 Computing Loan Sets from Lifetimes
To verify ownership-safety (perform "borrow-checking"), the Rust compiler does not explicitly build the loan sets of lifetimes (or provenances in Oxide terminology). The borrow checking algorithm performs a sort of flow-sensitive dataflow analysis that determines the range of code during which a lifetime is valid, and then checks for conflicts e.g. in overlapping lifetimes (see the non-lexical lifetimes RFC [].
However, Rust's borrow checker relies on the same fundamental language feature as Oxide to verify ownership-safety: outlives-constraints. For a given Rust function, Rust can output the set of outlives-constraints between all lifetimes in the function. These lifetimes are generated in the same manner as in Oxide, such as from inferred subtyping requirements or user-provided outlives-constraints. Then given these constraints, we compute loan sets via a process similar to the ownership-safety judgment described in Section 2.2. In short, for all instances of borrow expressions in the MIR program, we initialize . Then we propagate loans via until reaches a fixpoint.
4.3 Handling Ownership-Unsafe Code
Rust has a concept of raw pointers whose behavior is comparable to pointers in C. For a type T, an immutable reference has type &T, while an immutable raw pointer has type *const T. Raw pointers are not subject to ownership restrictions, and they can only be used in blocks of code demarcated as unsafe. They are primarily used to interoperate with other languages like C, and to implement primitives that cannot be proved as ownership-safe via Rust's rules.
Our pointer and mutation analysis fundamentally relies on ownership-safety for soundness. We do not try to analyze information flowing directly through unsafe code, as it would be subject to the same difficulties of C++ in Section 1. While this limits the applicability of our analysis, empirical studies have shown that most Rust code does not (directly) use unsafe blocks [][]. We further discuss the impact and potential mitigations of this limitation in Section 8.
5 Evaluation
Section 3 established that our analysis is sound. The next question is whether it is precise: how many spurious flows are included by our analysis? We evaluate two directions:
What if the analysis had more information? If we could analyze the definitions of called functions, how much more precise are whole-program flows vs. modular flows?
What if the analysis had less information? If Rust's type system was more like C++, i.e. lacking ownership, then how much less precise do the modular flows become?
To answer these questions, we created three modifications to Flowistry:
- The analysis recursively analyzes information flow within the definitions of called functions. For example, if calling a function
f(&mut x, y)wherefdoes not actually modifyx, then the Whole-Program analysis will not register a flow fromytox. - The analysis does not distinguish between mutable and immutable references. For example, if calling a function
f(&x), then the analysis assumes thatxcan be modified. - The analysis does not use lifetimes to reason about references, and rather assumes all references of the same type can alias. For example, if a function takes as input
f(x: &mut i32, y: &mut i32)thenxandyare assumed to be aliases.
The Whole-Program modification represents the most precise information flow analysis we can feasibly implement. The Mut-Blind and Pointer-Blind modifications represent an ablation of the precision provided by ownership types. Each modification can be combined with the others, representing possible conditions for evaluation.
To better understand Whole-Program, say we are analyzing the information flow for an expression f(&mut x, y) where f is defined as f(a, b) { (*a).1 = b; }. After analyzing the implementation of f, we translate flows to parameters of f into flows on arguments of the call to f. So the flow b -> (*a).1 is translated intoy -> x.1.
Additionally, if the definition of f is not available, then we fall back to the modular analysis. Importantly, due to the architecture of the Rust compiler, the only available definitions are those within the package being analyzed. Therefore even with Whole-Program, we cannot recurse into e.g. the standard library.
With these three modifications, we compare the number of flows computed from a dataset of Rust projects (Section 5.1) to quantitatively (Section 5.2) and qualitatively (Section 5.3) evaluate the precision of our analysis.
5.1 Dataset
To empirically compare these modifications, we curated a dataset of Rust packages (or "crates") to analyze. We had two selection criteria:
To mitigate the single-crate limitation of Whole-Program, we preferred large crates so as to see a greater impact from the Whole-Program modification. We only considered crates with over 10,000 lines of code as measured by the
clocutility [].To control for code styles specific to individual applications, we wanted crates from a wide range of domains.
After a manual review of large crates in the Rust ecosystem, we selected 10 crates, shown in Figure 2. We built each crate with as many feature flags enabled as would work on our Ubuntu 16.04 machine. Details like the specific flags and commit hashes can be found in the appendix.
| Project | Crate | Purpose | LOC | # Vars | # Funcs | Avg. Instrs/Func |
|---|---|---|---|---|---|---|
| rayon | Data parallelism library | 15,524 | 10,607 | 1,079 | 16.6 | |
| rustls | rustls | TLS implementation | 16,866 | 23,407 | 868 | 42.4 |
| sccache | Distributed build cache | 23,202 | 23,987 | 643 | 62.1 | |
| nalgebra | Numerics library | 31,951 | 35,886 | 1,785 | 26.7 | |
| image | Image processing library | 20,722 | 39,077 | 1,096 | 56.8 | |
| hyper | HTTP server | 15,082 | 44,900 | 790 | 82.9 | |
| rg3d | 3D game engine | 54,426 | 59,590 | 3,448 | 25.7 | |
| rav1e | Video encoder | 50,294 | 76,749 | 931 | 115.4 | |
| RustPython | vm | Python interpreter | 47,927 | 97,637 | 3,315 | 51.0 |
| Total: | 286,682 | 435,979 | 14,696 |
For each crate, we ran the information flow analysis on every function in the crate, repeated under each of the 8 conditions. Within a function, for each local variable , we compute the size of at the exit of the CFG — in terms of program slicing, we compute the size of the variable's backward slice at the function's return instructions. The resulting dataset then has four independent variables (crate, function, condition, variable name) and one dependent variable (size of dependency set) for a total of 3,487,832 data points.
Our main goal in this evaluation is to analyze precision, not performance. Our baseline implementation is reasonably optimized — the median per-function execution time was 370.24. But Whole-Program is designed to be as precise as possible, so its naive recursion is sometimes extremely slow. For example, when analyzing the GameEngine::render function of the rg3d crate (with thousands of functions in its call graph), the modular analysis takes 0.13s while the recursive analysis takes 23.18s, a 178 slowdown. Future work could compare our modular analysis to whole-program analyses across the precision/performance spectrum, such as in the extensive literature on context-sensitivity [].
5.2 Quantitative Results
We observed no meaningful patterns from the interaction of modifications — for example, in a linear regression of the interaction of Mut-Blind and Pointer-Blind against the size of the dependency set, each condition is individually statistically significant () while their interaction is not (). So to simplify our presentation, we focus only on four conditions: three for each modification individually active with the rest disabled, and one for all modifications disabled, referred to as Baseline.
5.2.1 Whole-Program
For Whole-Program, we compare against Baseline to answer our first evaluation question: how much more precise is a whole-program analysis than a modular one? To quantify precision, we compare the percentage increase in size of dependency sets for a given variable between two conditions. For instance, if Whole-Program computes and Baseline computes for some , then the difference is .
Figure 3-Left shows a histogram of the differences between Whole-Program and Baseline for all variables. In 94% of all cases, the Whole-Program and Baseline conditions produce the same result and hence have a difference of 0. In the remaining 6% of cases with a non-zero difference, visually enhanced with a log-scale in Figure 3-Right, the metric follows a right-tailed log-normal distribution. We can summarize the log-normal by computing its median, which is 7%. This means that within the 6% of non-zero cases, the median difference is an increase in size by 7%. Thus, the modular approximation does not significantly increase the size of dependency sets in the vast majority of cases.
Next, we address our second evaluation question: how much less precise is an analysis with weaker assumptions about the program than the Baseline analysis? For this question, we compare the size of dependency sets between the Mut-Blind and Pointer-Blind conditions versus Baseline. Figure 4 shows the corresponding histograms of differences, with the Whole-Program vs. Baseline histogram included for comparison.
First, the Mut-Blind and Pointer-Blind modifications reduce the precision of the analysis more often and with a greater magnitude than Baseline does vs. Whole-Program. 39% of Mut-Blind cases and 17% of Pointer-Blind cases have a non-zero difference. Of those cases, the median difference in size is 50% for Mut-Blind and 56% for Pointer-Blind.
Therefore, the information from ownership types is valuable in increasing the precision of our information flow analysis. Dependency sets are often larger without access to information about mutability or lifetimes.
5.3 Qualitative Results
The statistics convey a sense of how often each condition influences precision. But it is equally valuable to understand the kind of code that leads to such differences. For each condition, we manually inspected a sample of cases with non-zero differences vs. Baseline.
5.3.1 Modularity
One common source of imprecision in modular flows is when functions take a mutable reference as input for the purposes of passing the mutable permission off to an element of the input.
For example, the function crop from the image crate returns a mutable view on an image. No data is mutated, only the mutable permission is passed from whole image to sub-image. However, a modular analysis on the image input would assume that image is mutated by crop.
Another common case is when a value only depends on a subset of a function's inputs. The modular approximation assumes all inputs are relevant to all possible mutations, but this is naturally not always the case.
For example, this function from nalgebra returns a boolean whose value solely depends on the argument diag. However, a modular analysis of a call to this function would assume that self and b is relevant to the return value as well.
5.3.2 Mutability
The reason Mut-Blind is less precise than Baseline is quite simple — many functions take immutable references as inputs, and so many more mutations have to be
For instance, this function from hyper repeatedly calls an input function func with segments of an input buffer. Without a control-flow analysis, it is impossible to know what functions read_until will be called with. And so Mut-Blind must always assume that func could mutate buf. However, Baseline can rely on the immutability of shared references and deduce that func could not mutate buf.
5.3.3 Lifetimes
Without lifetimes, our analysis has to make more conservative assumptions about objects that could possibly alias. We observed many cases in the Pointer-Blind condition where two references shared different lifetimes but the same type, and so had to be classified as aliases.
For example, the link_child_with_parent_component function in rg3d takes mutable references to a parent and child. These references are guaranteed not to alias by the rules of ownership, but a naive pointer analysis must assume they could, so modifying parent could modify child.
5.4 Threats to Validity
Finally, we address the issue: how meaningful are the results above? How likely would they generalize to arbitrary code rather than just our selected dataset? We discuss a few threats to validity below.
Are the results due to only a few crates?
If differences between techniques only arose in a small number of situations that happen to be in our dataset, then our technique would not be as generally applicable. To determine the variation between crates, we generated a histogram of non-zero differences for the Baseline vs. Mut-Blind comparison, broken down by crate in Figure 5.
As expected, the larger code bases (e.g. rav1e and RustPython) have more non-zero differences than smaller codebases — in general the correlation between non-zero differences and total number of variables analyzed is strong, . However variation also exists for crates with roughly the same number of variables like
imageandhyper. Mut-Blind reduces precision for variables inhypermore often thanimage. A qualitative inspection of the respective codebases suggests this may be becausehypersimply makes greater use of immutable references in its API.These findings suggest that the impact of ownership types and the modular approximation likely do vary with code style, but a broader trend is still observable across all code.
Would Whole-Program be more precise with access to dependencies?
A limitation of our whole-program analysis is our inability to access function definitions outside the current crate. Without this limitation, it may be that the Baseline analysis would be significantly worse than Whole-Program. So for each variable analyzed by Whole-Program, we additionally computed whether the information flow for that variable involved a function call across a crate boundary.
Overall 96% of cases reached at least one crate boundary, suggesting that this limitation does occur quite often in practice. However, the impact of the limitation is less clear. Of the 96% of cases that hit a crate boundary, 6.6% had a non-zero difference between Baseline and Whole-Program. Of the 4% that did not hit a crate boundary, 0.6% had a non-zero difference. One would expect that Whole-Program would be the most precise when the whole program is available (no boundary), but instead it was much closer to Baseline.
Ultimately it is not clear how much more precise Whole-Program would be given access to all a crate's dependencies, but it would not necessarily be a significant improvement over the benchmark presented.
Is ownership actually important for precision?
The finding that Pointer-Blind only makes a difference in 17% of cases may seem surprisingly small. For instance, found in a empirical study of slices on C programs that "using a pointer analysis with an average points-to set size twice as large as a more precise pointer analysis led to an increase of about 70% in the size of [slices]."
A limitation of our ablation is that the analyzed programs were written to satisfy Rust's ownership safety rules. Disabling lifetimes does not change the structure of the programs to become more C-like — Rust generally encourages a code style with fewer aliases to avoid dealing with lifetimes. A fairer comparison would be to implement an application idiomatically in both Rust and Rust-but-without-feature-X, but such an evaluation is not practical. It is therefore likely that our results understate the true impact of ownership types on precision given this limitation.
6 Applications
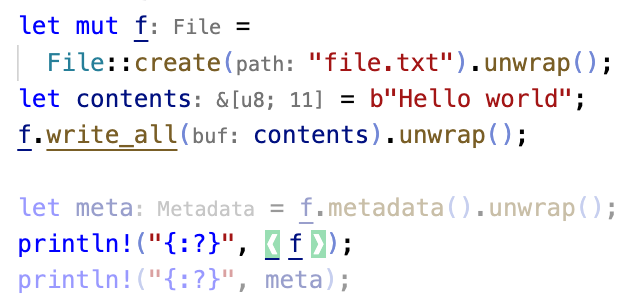

A program slicer integrated into VSCode. Above, the user selects a slicing criterion like the variable f. Then the slicer highlights the criterion in green, and fades out lines that are not part of the backward slice on f. For example, write_all mutates the file so it is in the slice, while metadata reads the file so it is not in the slice.
Below, the user can manipulate aspects of a program such as commenting out code related to timing. The user computes a forward slice on start, adds this slice to their selection (in blue), then tells the IDE to comments out all lines in the selection.

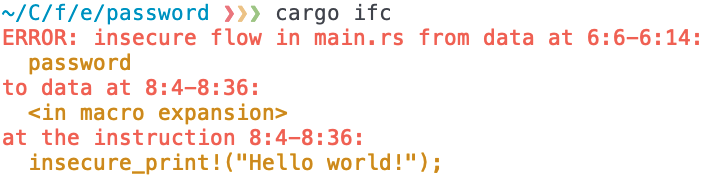
ifc_traits library exports a Secure for users to mark sensitive data, like Password, and insecure operations like insecure_print. Below, a compiler plugin invoked on the program checks for information flows from data with a type implementing Secure to insecure operations. Here insecure_print is conditionally executed based on a read from PASSWORD, so this flow is flagged.We have demonstrated that ownership can be leveraged to build an information flow analysis that is static, modular, sound, and precise. Our hope is that this analysis can serve as a building block for future static analyses. To bootstrap this future, we have used Flowistry to implement prototypes of a program slicer and an IFC checker, shown in Figure 6.
The program slicer in Figure 6a is a VSCode extension that fades out all lines of code that are not relevant to the user's selection, i.e. not part of the modular slice. Rather than present a slice of the entire program like in prior slicing tools, we can use Flowistry's modular analysis to present lightweight slices of just within a given function. Users can apply the slicer for comprehension tasks such as reducing the scope of a bug, or for refactoring tasks such as removing an aspect of a program like timing or logging.
The IFC checker in Figure 6b is a Rust library and compiler plugin. It provides the user a library with the traits Secure and Insecure to indicate the relative security of data types and operations. Then the compiler plugin uses Flowistry to determine whether information flows from Insecure variables to Secure variables. Users can apply the IFC checker to catch sensitive data leaks in an application. This prototype is purely intraprocedural, but future work could build an interprocedural analysis by using Flowistry's output as procedure summaries in a larger information flow graph.
7 Related Work
Our work draws on three core concepts: information flow, modular static analysis, and ownership types.
7.1 Information Flow
Information flow has been historically studied in the context of security, such as ensuring low-security users of a program cannot infer anything about its high-security internals. Security-focused information flow analyses have been developed for Java [], Javascript [], OCaml [], Haskell [], and many other languages.
Each analysis satisfies some, but not all, of our requirements from Section 1. For instance, the JFlow [] and Flow-Caml [] languages required adding features to the base language, violating our second requirement. Some methods like that of for Javascript rely on dynamic analysis, violating our third requirement. And Haskell only supports effects like mutation through monads, violating our first requirement.
Nonetheless, we draw significant inspiration from mechanisms in prior work. Our analysis resembles the slicing calculus of . The use of lifetimes for modular analysis of functions is comparable to security annotations in Flow-Caml []. The CFG analysis draws on techniques used in program slicers, such as the LLVM dg slicer [].
7.2 Modular Static Analysis
The key technique to making static analysis modular (or "compositional" or "separate") is symbolically summarizing a function's behavior, so that the summary can be used without the function's implementation. Starting from and , one approach has been to design a system of "procedure summaries" understood by the static analyzer and distinct from the language being analyzed. This approach has been widely applied for static analysis of null pointer dereferences [], pointer aliases [], data dependencies [], and other properties.
Another approach, like ours, is to leverage the language's type system to summarize behavior. showed that an effect system could be used for a modular control-flow analysis. Later work in Haskell used its powerful type system and monadic effects to embed many forms of information flow control into the language [][][][].
7.3 Ownership Types
Rust and Oxide's conceptions of ownership derive from and . For instance, the Cyclone language of Grossman et al. uses regions to restrict where a pointer can point-to, and uses region variables to express relationships between regions in a function's input and output types. A lifetime is similar in that it annotates the types of pointers, but differs in how it is analyzed.
Recent works have demonstrated innovative applications of Rust's type system for modular program analysis. embed Rust programs into a separation logic to verify pre/post conditions about functions. use Rust's ownership-based guarantees to implement more aggressive program optimizations.
Closer to our domain, implemented a prototype IFC system for Rust by lowering programs to LLVM and verifying them with SMACK [], although their system is hard to contrast with ours given the high-level description in their paper. implemented a static taint analysis for Rust, although it is not field-sensitive, alias-sensitive, or modular.
8 Discussion
Looking forward, two interesting avenues for future work on Flowistry are improving its precision and addressing soundness in unsafe code. For instance, the lifetime-based pointer analysis is sound but imprecise in some respects. Lifetimes often lose information about part-whole relationships. Consider the function that returns a mutable pointer to a specific index in a vector:
These lifetimes indicate only that the return value points to something in the input vector. The expressions v.get_mut(i) and v.get_mut(i + 1) are considered aliases even though they are not. Future work could integrate Flowistry with verification tools like Prusti [] to use abstract interpretation for a more precise pointer analysis in such cases.
Additionally, Rust has many libraries built on unsafe code that can lose annotations essential to information flow, such as interior mutability. For example, shared-memory concurrency in Rust looks like this:
Arc::clone does not share a lifetime between its input and output, so a lifetime-based pointer analysis therefore cannot deduce that n2 is an alias of n, and Flowistry would not recognize that the mutation on line 3 affects n. Future work can explore how unsafe libraries could be annotated with the necessary metadata needed to analyze information flow, similar to how RustBelt [] identifies the pre/post-conditions needed to ensure type safety within unsafe code.
Overall, we are excited by the possibilities created by having a practical information flow analysis that can run today on any Rust program. Many exciting systems for tasks like debugging [], example generation [], and program repair [] rely on information flow in some form, and we hope that Flowistry can support the development of these tools.